ワインバーグ・サラム理論 note08: $\nu_\mu + e \rightarrow \nu_\mu + e$ 散乱など

今回は$\nu_\mu + e \rightarrow \nu_\mu + e$ 散乱過程を考える。これはnote05で議論した中性カレントだけが関与する散乱過程であり、相互作用のラグランジアンは

$$\begin{eqnarray} - \L_I &=& \frac{g^2}{2 M_W^2} J_\mu J_\mu \\ J_\mu &=& g_L^\nu \bar{\nu}_{L}^{(\mu )} \ga_\mu \nu_{L}^{(\mu )} + g_L^e \bar{e}_L \ga_\mu e_L + g_R^e \bar{e}_R \ga_\mu e_R + \cdots \end{eqnarray}$$

で与えられる。ただし、中性カレントの一般形はnote05の式(11)で表され、$g_L^\nu = \hf$, $g_L^e = -\hf - \sin^2 \th_W$, $g_R^e = - \sin^2 \th_W$である。$\nu_\mu + e \rightarrow \nu_\mu + e$ 散乱に関与する$\L_I$は

$$\begin{eqnarray} - \L_I &=& \frac{g^2}{2 M_W^2} 2 g_L^\nu \bar{\nu}_L \ga_\mu \nu_L \left( g_L^e \bar{e}_L \ga_\mu e_L + g_R^e \bar{e}_R \ga_\mu e_R \right) \\ &=& 2 \frac{G_F}{\sqrt{2}} g_L^\nu \bar{\nu} \ga_\mu ( 1 - \ga_5 ) \nu \left[ g_L^e \bar{e} \ga_\mu (1 - \ga_5 ) e + g_R^e \bar{e} \ga_\mu (1 + \ga_5 ) e \right] \end{eqnarray} \tag{1}$$

と表せる。ただし、$\frac{g^2}{8 M_W^2} = \frac{G_F}{\sqrt{2}}$である。

これより散乱振幅は

$$\begin{eqnarray} \M &=&  - \int \L_I d^4 x \\ &=& 2 \frac{G_F}{\sqrt{2}} g_L^\nu \bar{\nu}_{k^\prime} \ga_\mu ( 1 - \ga_5 ) \nu_{k} \left[ g_L^e \bar{e}_{p^\prime \la^\prime} \ga_\mu (1 - \ga_5 ) e_{p \la} \right. \\ && ~~~~~~~~\left. + g_R^e \bar{e}_{p^\prime \la^\prime} \ga_\mu (1 + \ga_5 ) e_{p \la} \right]  (2\pi)^4 \del ( k + p - k^\prime - p^\prime ) \end{eqnarray}$$

となる。この2乗を取ると

$$\begin{eqnarray} | \M |^2 &=& 4 \left( \frac{G_F}{\sqrt{2}} \right)^2 ( g_L^\nu )^2 \Big[ \bar{\nu}_{k^\prime} \ga_\mu ( 1 - \ga_5 ) \nu_{k} \bar{\nu}_{k} \ga_\al ( 1 - \ga_5 ) \nu_{k^\prime}  \Big] \\ && ~ \times  \Big[ ( g_L^e )^2 \bar{e}_{p^\prime} \ga_\mu (1 - \ga_5 ) e_{p } \bar{e}_{p} \ga_\al (1 - \ga_5 ) e_{p^\prime} + ( g_R^e )^2 \bar{e}_{p^\prime } \ga_\mu (1 + \ga_5 ) e_{p } \bar{e}_{p} \ga_\al (1 + \ga_5 ) e_{p^\prime } \Big] \\ && ~~~~~~~ \times (2 \pi )^4 \del (k + p - k^\prime - p^\prime ) VT \end{eqnarray} \tag{2}$$

ただし、$VT$は時空間体積。また、偏極のラベル$\la, \la^\prime$を省略した。フェルミ粒子の伝播関数は

$$\bra f (x) \bar{f} (y) \ket =  \int \frac{d^4 p}{(2 \pi)^4} \frac{-i{p \!\!\! /}}{p^2} e^{ip(x-y) }$$

正の振動数部分は$\frac{{p \!\!\! /}}{2 E_p} \frac{d^3 p}{(2 \pi )^3}$となる。よって、運動量表示では$\bra \nu_k \bar{\nu}_k \ket = {k \!\!\! /}$として相空間因子$\frac{d^3 k}{(2 \pi )^3}\frac{ 1 }{2 E_k }$を付随させればよい。入射電子のスピンについては平均をとる。これより(2)は

$$\begin{eqnarray} | \M |^2 &=& 2\left( \frac{G_F}{\sqrt{2}} \right)^2 ( g_L^\nu )^2  2 \tr \big[ \ga_\mu {k \!\!\! /} \ga_\al {k \!\!\! /}^\prime ( 1 + \ga_5 )  \big] \\ && ~ \times 2 \Big[ ( g_L^e )^2 \tr \big[ \ga_\mu {p \!\!\! /} \ga_\al  {p \!\!\! /}^\prime (1 + \ga_5 ) \big] + ( g_R^e )^2 \tr \big[ \ga_\mu {p \!\!\! /} \ga_\al  {p \!\!\! /}^\prime (1 - \ga_5 )\big]   \Big] \\ && ~ \times (2 \pi )^4 \del (k + p - k^\prime - p^\prime ) VT   \left[ \frac{d^3 k}{(2 \pi )^3}\frac{ 1 }{2 E_k }  \frac{d^3 p}{(2 \pi )^3}\frac{ 1 }{2 E_p } \right] \left[ \frac{d^3 k^\prime}{(2 \pi )^3}\frac{ 1 }{2 E_{k^\prime} }  \frac{d^3 p^\prime }{(2 \pi )^3}\frac{ 1 }{2 E_{p^\prime} } \right] \end{eqnarray} \tag{3}$$

と書ける。$n^\nu$, $n^e$を整数、$V= L^3$として、$k = \frac{2\pi n^{\nu}}{L}$, $p \frac{2\pi n^{e}}{L}$とおく。$n^\nu$, $n^e$を固定値として入射状態を固定すると

$$\begin{eqnarray} | \M |^2 &=& 2\left( \frac{G_F}{\sqrt{2}} \right)^2 ( g_L^\nu )^2  2 \tr \big[ \ga_\mu {k \!\!\! /} \ga_\al {k \!\!\! /}^\prime ( 1 + \ga_5 )  \big] \\ && ~ \times 2 \Big[ ( g_L^e )^2 \tr \big[ \ga_\mu {p \!\!\! /} \ga_\al  {p \!\!\! /}^\prime (1 + \ga_5 ) \big] + ( g_R^e )^2 \tr \big[ \ga_\mu {p \!\!\! /} \ga_\al  {p \!\!\! /}^\prime (1 - \ga_5 )\big]   \Big] \\ && ~ \times (2 \pi )^4 \del (k + p - k^\prime - p^\prime ) \frac{T}{V}   \frac{ 1 }{2 E_k }  \frac{ 1 }{2 E_p } \left[ \frac{d^3 k^\prime}{(2 \pi )^3}\frac{ 1 }{2 E_{k^\prime} }  \frac{d^3 p^\prime }{(2 \pi )^3}\frac{ 1 }{2 E_{p^\prime} } \right] \end{eqnarray} \tag{4}$$

散乱断面積$d \si$は散乱確率$\frac{|\M |^2}{T}$をフラックス$\frac{v}{V}$で割ったものである。ここで$v$は$\nu_\mu$と$e$の相対速度である。入射電子の静止系で考えると$v=c$（光速、$c=1$）とおけるので、

$$d \si = \int \frac{1}{2E_k}\frac{ 1 }{2 E_p } 2\left( \frac{G_F}{\sqrt{2}} \right)^2 ( g_L^\nu )^2  L_{\mu\al} (k, k^\prime ) \Big[  ( g_L^e )^2 L_{\mu\al} (p, p^\prime ) + ( g_R^e )^2 R_{\mu\al} (p, p^\prime ) \Big] d \mbox{(phase)} \tag{5}$$

$$\begin{eqnarray} L_{\mu\al} (k, k^\prime ) &=&  2 \tr \big[ \ga_\mu {k \!\!\! /} \ga_\al {k \!\!\! /}^\prime ( 1 + \ga_5 )  \big]  = 8 \big[ k_\mu k_\al^\prime + k_\al k_\mu^\prime -(k \cdot k^\prime ) \del_{\mu\al} + \ep_{\mu\nu\al\bt} k_\nu k_\bt^\prime  \big]  \\ R_{\mu\al} (p, p^\prime )  &=&  2 \tr \big[ \ga_\mu {p \!\!\! /} \ga_\al  {p \!\!\! /}^\prime (1 - \ga_5 )\big]  = 8 \big[ p_\mu p_\al^\prime + p_\al p_\mu^\prime -(p \cdot p^\prime ) \del_{\mu\al} - \ep_{\mu\nu\al\bt} p_\nu p_\bt^\prime \big]   \end{eqnarray} \tag{6}$$

ただし、

$$\begin{eqnarray} \tr \big[ \ga_\mu \ga_\nu \ga_\al \ga_\bt \big] &=& 4 ( \del_{\mu\nu}\del_{\al\bt} - \del_{\mu\al}\del_{\nu\bt} + \del_{\mu\bt}\del_{\nu \al} ) \\ \tr \big[ \ga_\mu \ga_\nu \ga_\al \ga_\bt \ga_5 \big] &=& 4 \ep_{\mu\nu\al\bt}  \end{eqnarray}$$

を用いた。また、(5)の相空間因子は

$$\begin{eqnarray} \int d \mbox{(phase)}&=& \int (2 \pi )^4 \del^{(4)} (k + p - k^\prime - p^\prime ) \frac{d^3 k^\prime}{(2 \pi )^3}\frac{ 1 }{2 E_{k^\prime} }  \frac{d^3 p^\prime }{(2 \pi )^3}\frac{ 1 }{2 E_{p^\prime} } \end{eqnarray}$$

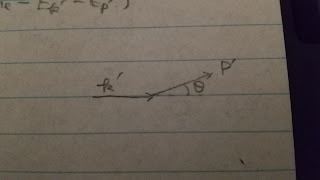
$\vec{k}^\prime$と$\vec{p}^\prime$の成す角を$\th$とおく。

$$\begin{eqnarray} E_k &=& |\vec{k}| = k \\ E_p &=& m_e \\ E_{k^\prime} &=& |\vec{k} - \vec{p}^\prime | = \sqrt{k^2 -2kp^\prime cos \th + p^2 } \\ E_{p^\prime} &=& \sqrt{ |\vec{p}^{\prime}|^{2} + m_e^2} = \sqrt{p^{\prime 2} + m_e^2}\\ \frac{d E_{p^\prime}}{d p^\prime} &=& \frac{p^\prime}{\sqrt{p^{\prime 2} + m_e^2}} = \frac{p^\prime}{E_{p^\prime} } \end{eqnarray}$$
に注意すると

$$\begin{eqnarray} \int d \mbox{(phase)}&=&  \left. \frac{1}{16\pi^2} \int \del ( E_k + m_e - E_{k^\prime} = E_{p^\prime} ) \frac{d^3 P^\prime}{E_{p^\prime}E_{k^\prime}} \right|_{\vec{k}^\prime = \vec{k} - \vec{p}^\prime }  \\ &=& \frac{1}{8\pi} \int_{-1}^{1} d (\cos \th ) \int p^{\prime 2} d p^\prime \frac{1}{E_{p^\prime}E_{k^\prime}}\del ( E_k + m_e - E_{k^\prime} = E_{p^\prime} )  \\ &=&   \frac{1}{8\pi} \int d (\cos \th )  ~ \del \left( f(\cos \th ) \right) ~ \frac{p^\prime  d E_{p^\prime}}{E_{k^\prime}} \\ &=&  \frac{1}{8\pi} \frac{1}{\frac{E_k p^\prime}{E_{k^\prime}}} \frac{p^\prime  d E_{p^\prime}}{E_{k^\prime}}  = \frac{1}{8 \pi} \frac{d E_{p^\prime}}{E_k} \end{eqnarray}\tag{7}$$

ただし、

$$\begin{eqnarray} f(\cos \th ) &=& k + m_e -  \sqrt{k^2 -2kp^\prime cos \th + p^2 } - \sqrt{p^{\prime 2} + m_e^2} \\  f^\prime (\cos \th ) &=& \frac{k p^\prime}{\sqrt{k^2 -2kp^\prime cos \th + p^2 }} =  \frac{E_k p^\prime}{E_{k^\prime}} \end{eqnarray}$$

を用いた。

式(6)より

$$\begin{eqnarray} L_{\mu\al} (k, k^\prime ) L_{\mu\al} (p, p^\prime ) &=& 64 \Big[ \big(  k_\mu k_\al^\prime + k_\al k_\mu^\prime - (k \cdot k^\prime ) \del_{\mu \al} \big) \big( p_\mu p_\al^\prime + p_\al  p_\mu^\prime - (p \cdot p^\prime ) \del_{\mu \al} \big) + \ep_{\mu\nu\al\bt} \ep_{\mu \si \al\tau} k_\nu k_\bt^\prime p_\si p_\tau^\prime \Big] \\ &=&64 \Big[ 2(k \cdot p) (k^\prime \cdot p^\prime ) + 2(k \cdot p^\prime) (k^\prime \cdot p ) + 2  (k \cdot p) (k^\prime \cdot p^\prime ) - 2(k \cdot p^\prime) (k^\prime \cdot p )\Big]\end{eqnarray}$$

ここで、$k^2 = k^{\prime 2} = 0$, $p^2 = p^{\prime 2} = - m_e^2$, $k+p = k^\prime + p^\prime$から

$$k \cdot p = k^\prime \cdot p^\prime ~, ~~~~~~ k \cdot p^\prime = k^\prime \cdot p$$

なので、

$$\begin{eqnarray} L_{\mu\al} (k, k^\prime ) L_{\mu\al} (p, p^\prime ) &=& 256 (k \cdot p) (k^\prime \cdot p^\prime ) = 256 (k \cdot p )^2 = 256 (E_k m_e )^2 \\ L_{\mu\al} (k, k^\prime ) R_{\mu\al} (p, p^\prime ) &=& 256 (k \cdot p^\prime ) (k^\prime \cdot p) = 256 (k^\prime \cdot p )^2 = 256 (E_{k^\prime} m_e )^2 \end{eqnarray}$$

が得られる。したがって、(5)は

$$\begin{eqnarray} \frac{d \si}{d E_{p^\prime}} &=& \frac{1}{32 \pi}  \frac{1}{E_k^2  m_e} G_F^2 (g_L^\nu )^2 256 \big[(g_L^e )^2 (E_k m_e )^2  L  + (g_R^e )^2 (E_{k^\prime} m_e )^2  \big] \\ &=& \frac{8G_F^2  m_e }{\pi} (g_L^\nu )^2 \left[ (g_L^e )^2 + (g_R^e )^2 \left( \frac{E_{k^\prime}}{E_k} \right)^2 \right] \end{eqnarray}\tag{8}$$

となる。慣習的な（エネルギー遷移比率の）スケール変数

$$y = \frac{E_{p^\prime}}{E_k} ~~~~~~ (E_k \gg m_e )$$

を用いると

$$\frac{d \si ( \nu_\mu e) }{d y } = \frac{8G_F^2 }{\pi}  m_e E_k (g_L^\nu )^2 \big[ (g_L^e )^2 + (g_R^e )^2 (1 -y )^2 \big]  \tag{9}$$

となり、散乱断面積は

$$d \si ( \nu_\mu e) = \frac{8G_F^2 }{\pi}  m_e E_k (g_L^\nu )^2 \left[ (g_L^e )^2 +  \frac{1}{3} (g_R^e )^2  \right]  \tag{10}$$

で与えられる。式(9)の$(1-y)^2$が式(10)から$\frac{1}{3}$因子が出てくるが、この項は入射ニュートリノと反対のヘリシティをもつ項に対応する。よって、反ニュートリノの散乱過程$\bar{\nu}_\mu e \rightarrow \bar{\nu}_\mu e$の散乱断面積は同様の解析から

$$d \si ( \bar{\nu}_\mu e) = \frac{8G_F^2 }{\pi}  m_e E_k (g_L^\nu )^2 \left[ \frac{1}{3} (g_L^e )^2 +   (g_R^e )^2  \right]  \tag{11}$$

となることが類推できる。

これまで$\nu_\mu$と$e$の散乱を考えたが、同一世代の$\nu_e$と$e$の散乱過程$\bar{\nu}_e e \rightarrow \bar{\nu}_e e$の場合は、荷電カレントと中性カレントの両方が寄与する。

この場合、散乱断面積は次のように計算できる。

$$\begin{eqnarray}d \si ( \nu_e e) &=& \frac{8G_F^2 }{\pi}  m_e E_k (g_L^\nu )^2 \left[ ( 1 + g_L^e )^2 +  \frac{1}{3} (g_R^e )^2  \right]   \\ d \si ( \bar{\nu}_e e) &=& \frac{8G_F^2 }{\pi}  m_e E_k (g_L^\nu )^2 \left[ \frac{1}{3} ( 1 + g_L^e )^2 +   (g_R^e )^2  \right]   \end{eqnarray} \tag{12}$$

$( g_L^e )^2$ではなく$( 1 + g_L^e )^2$となっているのは荷電カレントの効果であることに注意。

Wボソン崩壊過程

次に$W_\mu^- \rightarrow e + \bar{\nu}$の崩壊過程を考える。

$W^{\pm}$ボソンとフェルミ粒子の結合はnote05の式(4)で見たように荷電カレント$W^{\pm}$と荷電カレントの相互作用で記述される。多世代モデルの場合クォーク・レプトンセクターでの$W^{\pm}$と荷電カレントの相互作用はそれぞれnote06の式(7), (13)で表される。

$$L_{W} = - \frac{i g}{2 \sqrt{2}} W_\mu^+ \left[ \Big( \bar{\nu}_e ~ \bar{\nu}_\mu ~ \bar{\nu}_\tau \Big) \ga_\mu (1- \ga_5 )  \begin{pmatrix} e \\ \nu \\ \tau \end{pmatrix} + \Big(\bar{u} ~ \bar{c} ~ \bar{t} \Big) \ga_\mu (1- \ga_5 ) V \begin{pmatrix} d \\ s \\ b \end{pmatrix} \right] + h.c. \tag{13}$$

ただし、$V$はCKM行列、レプトンセクターでは世代間の混合は無いとした。この相互作用項(13)を用いて様々な崩壊モードを計算できる。例えば、$W_\mu^- (k) \rightarrow e(p) + \bar{\nu} (q)$を考えよう。行列要素は

$$\M = \frac{i g}{2 \sqrt{2} } \bar{e}^s (p) \ga_\mu (1 - \ga_5 ) \nu^{s'} (q) \ep^\mu ( k , \la )$$

ただし、$\ep^\mu ( k , \la )$は$W$ボソンの偏極ベクトル。フェルミオンのスピンについて和を取り、$W$ボソンの偏極の平均をとると

$$\frac{1}{3} \sum_{\la, s, s'} | \M |^2 = \frac{1}{3} \frac{g^2}{8} \sum_\la \ep_\mu ( k, \la ) \ep_\nu^* (k , \la ) \Big[ \sum_{s, s'} \bar{e}^s (p) \ga_\mu (1 - \ga_5 ) \nu^{s'} (q) \bar{\nu}^{s'} (q) \ga_\nu (1 - \ga_5 ) e^{s} (p) \Big] \tag{14}$$

となる。ここで、

$$\begin{eqnarray} \sum_{\la =0, \pm 1} \ep_\mu ( k, \la ) \ep_\nu^* (k , \la )  &=&  \del_{\mu\nu} + \frac{k_\mu k_\nu}{M_W^2} \tag{15} \\ \sum_{s} \bar{e}_\al^s (p) e_\bt^s (p) &=& ( {p \!\!\! /} + m_e )_{\al\bt} \\ \sum_{s'} \nu_{\al}^{s'} (q) \bar{\nu}_{\bt}^{s'} (q) &=& ({q \!\!\! /})_{\al \bt} \end{eqnarray}$$

$$\begin{eqnarray} && \sum_{s, s'} \bar{e}^s (p) \ga_\mu (1 - \ga_5 ) \nu^{s'} (q) \bar{\nu}^{s'} (q) \ga_\nu (1 - \ga_5 ) e^{s} (p)  \\ &=& \tr \Big[ ( {p \!\!\! /} + m_e ) \ga_\mu (1 - \ga_5 ) {q \!\!\! /} \ga_\nu ( 1 - \ga_5 ) \Big] \\ &=& 2 \tr \Big[ ( {p \!\!\! /} + m_e ) \ga_\mu {q \!\!\! /} \ga_\nu ( 1 - \ga_5 ) \Big] \\ &=& 2 p_\al q_\bt \tr \Big[ ( \ga_\al \ga_\mu \ga_\bt \ga_\nu ( 1 - \ga_5 ) \Big] \\ &=& 8 p_\al q_\bt \big( \del_{\al \mu} \del_{\bt \nu} + \del_{\al \nu}\del_{\bt \mu} - \del_{\al \bt} \del_{\mu \nu} - \ep_{\al \mu \bt \nu} \big) \\ &=& 8 \Big[ p_\mu q_\nu + p_\nu q_\mu - \del_{\mu\nu} ( p \cdot q ) - \ep_{\al \mu \bt \nu} p_\al q_\bt \Big] \tag{16} \end{eqnarray}$$

ただし、$\tr ( \mbox{奇数個の$\ga$} ) =0$, $\tr (\ga_\mu \ga_\nu \ga_\al \ga_5 )=0$を使った。(16)は$\mu, \nu$について対称であるが$\ep_{\al \mu \bt \nu}$は添え字について完全反対称であるので、(16)の最後の項は(14)に寄与しない。よって、

$$\begin{eqnarray}  \frac{1}{3} \sum_{\la, s, s'} | \M |^2 &=& \frac{g^2}{3} \big[ p_\mu q_\nu + p_\nu q_\mu - \del_{\mu\nu} ( p \cdot q ) \big] \left(  \del_{\mu\nu} + \frac{k_\mu k_\nu}{M_W^2} \right) \\ &=& \frac{g^2}{3 M_W^2} \Big[ 2 (p \cdot k )( q \cdot k ) - M_W^2 (p \cdot q ) \Big] \end{eqnarray}$$

ここで、$k^2 = -M_W^2$, $p+q = k$なので$m_e (\ll M_W )$を無視すると

$$\frac{1}{3} \sum_{\la, s, s'} | \M |^2  \simeq \frac{1}{3}g^2 M_W^2 \tag{17}$$

を得る。

このとき、$W$ボソンの静止系 $(E_k = M_W, E_p  =\sqrt{p^2 + m_e^2}, E_q =|\vec{q}| = q)$ で崩壊確率$\Ga_{e} ( W^- \rightarrow e \bar{\nu}_e )$は

$$\begin{eqnarray} \Ga_e  ( W^- \rightarrow e \bar{\nu}_e )&=& \frac{1}{2 M_W} \int (2 \pi )^4 \del^{(4)} (k - p -q) \frac{1}{3} \sum_{\la, s, s'} | \M |^2 \frac{d^3 p}{(2 \pi)^3 2 E_p} \frac{d^3 q}{(2 \pi)^3 2 E_q} \\ &=& \left. \frac{1}{2 M_W} \frac{g^2 }{3 }M_W^2  \frac{1}{(2 \pi)^2} \int \del ( M_W - E_p - E_q) \frac{d^3 p} {2 E_p 2 E_q} \right|_{\vec{p}+\vec{q} = 0 } \\ &=&  \frac{g^2 M_W }{6} \frac{4 \pi}{16 \pi^2} \int \del \left( M_W - \sqrt{p^2 + m_e^2} - p \right) \frac{p^2 d p} {p \sqrt{p^2 + m_e^2}} \end{eqnarray}$$

ここで、

$$\begin{eqnarray} f(p) &=& M_W - \sqrt{p^2 + m_e^2} - p \\ f^\prime (p) &=& \frac{-p}{\sqrt{p^2 + m_e^2}} -1 \\ \int \del \left( M_W - \sqrt{p^2 + m_e^2} - p \right) \frac{p^2 d p} {p \sqrt{p^2 + m_e^2}} &=& \frac{1}{\frac{p+ \sqrt{p^2 + m_e^2} } { \sqrt{p^2 + m_e^2}}}\frac{p} { \sqrt{p^2 + m_e^2}} \simeq \hf ~~~ (p^2 \gg m_e^2 )\end{eqnarray}$$

なので

$$\Ga_e  ( W^- \rightarrow e \bar{\nu}_e ) \simeq \frac{g^2 M_W}{48\pi} = \frac{G_F}{\sqrt{2}} \frac{M_W^3}{6\pi} \tag{18}$$

となる。ただし、$\frac{G_F}{\sqrt{2}} = \frac{g^2}{8 M_W^2}$を用いた。この崩壊確率はフェルミ定数$G_F$に比例する。通常、弱い相互作用の崩壊確率は$G_F^2$に比例するので、この過程はsemi-weakな崩壊と言える。

最後に3世代に拡張して崩壊確率を計算する。レプトンへの崩壊はこれまでと同様に

$$\Ga_e  ( W^- \rightarrow e \bar{\nu}_e ) = \Ga_\mu  ( W^- \rightarrow \mu \bar{\nu}_\mu  ) = \Ga_\tau ( W^- \rightarrow \tau \bar{\nu}_\tau )$$

となる。クォークへの崩壊は荷電カレントが

$$J_\mu^+ = \bar{E}_L^i \ga_\mu N_L^i + V_{ij} \bar{D}_L^i \ga_\mu U_L^j$$

なので、終状態のクォーク対について和を取ること以外は$\Ga_e$と同じである。例えば、

$$\Ga ( W^- \rightarrow \bar{u} d ) \simeq 3 |V_{11}|^2  \frac{G_F}{\sqrt{2}} \frac{M_W^3}{6\pi}$$

となる。ここで、$V_{ij}$はCKM行列の要素、因子３は色の数（クォークがQCDの$SU(3)$群の3重項であること）を表す。2世代の場合は$|V_{ij}| = 1$となる。よって、$W^-$からクォークへの崩壊確率は

$$\Ga (W^- \rightarrow \mbox{all quarks} ) \simeq 3 \sum_{\mbox{allowed}~(i,j) } |V_{ij}|^2　\frac{G_F}{\sqrt{2}} \frac{M_W^3}{6\pi}$$

と表せる。

Zボソン崩壊過程

$Z$ボソンは冒頭で示した中性カレントと相互作用するので、$Z \rightarrow \nu \bar{\nu}$ の崩壊確率も動力学的に全く同様に計算できる。

$$\Ga (Z \rightarrow \nu \bar{\nu}) \simeq \hf \frac{G_F}{\sqrt{2}} \frac{M_Z^3}{6\pi}  \simeq 0.18 ~ GeV$$

ここで、$\hf$因子は$Z$ボゾンと中性カレントとの相互作用

$$-i \frac{g}{\cos \th_W} Z_\mu \hf \bar{\nu}_L \ga_\mu \nu_L$$

と$W^-$ボソンと荷電カレントとの相互作用

$$-i \frac{g}{\sqrt{2}} W_\mu^-  \bar{e}_L \ga_\mu \nu_L$$

の係数が異なることに起因する。つまり、$g^\prime$の効果であると考えられる。$Z \rightarrow \nu \bar{\nu}$ は中性の崩壊過程なので精度よく観測できる。よって、観測値$\Ga_{exp.} ( Z \rightarrow \nu \bar{\nu})$を用いてニュートリノの数 $N_\nu$ を推測できる。

$$\Ga_{exp.} ( Z \rightarrow \nu \bar{\nu})  = N_\nu \frac{G_F}{\sqrt{2}} \frac{M_Z^3}{12 \pi}$$  

実験値から $N_\nu \simeq 3$ が知られている。