最近読んだ本：「フランクリンの凧」の一般化！

「フランクリンの凧」と聞いてピンとくる人は中学の時に平面幾何が好きだった人ですよね。今回はそんな人向けのエントリーです。私も中学生の時は平面幾何が好きで矢野健太郎先生の名著『幾何の有名な定理』

をよく読んだものです。今でも本棚に飾っています。平面幾何を深めていくと結局平面上の点を複素平面上で解析的に考えれば補助線などに頼らなくても機械的に平面幾何を理解できるということに気づきます。つまりガウス平面の導入です。ガウス平面は単に２次元上のデカルト座標$(x, y)$を虚数 $z= x + i y$ として考え、$x$ 座標、$y$ 座標をそれぞれ実軸、虚軸とみなすことで得られます。こうするとガウス平面上での点 $z$ を極座標表示 $z = r e^{i \th} = r ( \cos \th + i \sin \th )$ することが出来、角度 $\th$ の議論がしやすくなります。極座標表示を使うと単位円の場合($r = 1$)に $z^n = e^{i n \th } = ( \cos \th + i \sin \th )^n =  \cos n \th + i \sin n \th$ となることは容易にわかりますがこれはド・モアブルの定理と呼ばれています。この辺りの話は三角関数が出てくるので高校で習います。この頃には、三角関数の加法定理や余弦定理などを覚えることで忙しく平面幾何なんて算数だよなあなんて感じるかもしれませんが、中学生の時に知った九点円の話のようなシンプルだけどエレガントで美しい結果はやはり魅力的です。

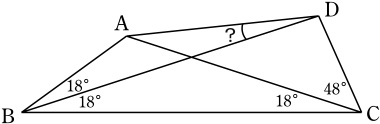
そんな平面幾何の問題であれは何だったのだろうとたまに思い出すのが「フランクリンの凧」と呼ばれる解法で角度を求める問題です。有名な問題なので検索をかけてみると

http://ytsumura.cocolog-nifty.com/blog/2004/08/post_3.html

からの一連の投稿で昔の中学生たちが活発に議論しているのを興味深く読みました。また、こちらのサイト

https://tsujimotter.hatenablog.com/entry/langley-problem

を覗いてみるとなんと素晴らしいタイトルの本が紹介されていました。斉藤浩著『ラングレーの問題にトドメをさす!―4点の作る小宇宙完全ガイド』

です（税別2700円）。少しためらいましたがアマゾンで購入しました。本が配送されるまで著者のサイトで所謂ラングレー問題あるいは４点角問題について復習しました。こちら

https://www.gensu.co.jp/saito/challenge/langley.html

の証明例８で「フランクリンの凧」という通称のもとになった証明が紹介されています。類似のラングレー問題一覧ページ

https://www.gensu.co.jp/saito/challenge/index.html

から一問を適当に選んで

中学生になった気分で手を出してみました。しかし、いくら考えても全く歯が立ちません。理論物理でPhDまで取得したのに中学生の問題が解けないのか～と己を奮い立たせて頑張りましたがダメでした。仕方なく解答を見ると

2013年夏の富士山リベンジ登山：念願の剣ヶ峰到達、お鉢めぐり成就！

前回のエントリーのとおり2012年の富士山初登山ではペース配分も無茶苦茶に登り始め結局、高山病になり下山後に吐いてしまうという大失態＆大失敗登山という散々なものでした。リベンジの機会を窺っていた翌年、晴天の平日に再度チャレンジすることにしました。今回は高山病になることも見越して電車・バスでアクセス、5合目からの帰りの最終バスが18時発ということなのでそれまでに帰れるよう、ペース配分、とくに呼吸に意識して登りました。

2012年夏の富士山初登山で失敗した件

新型ウイルスの影響で今年の富士山登山道が閉鎖になったそうです。

https://www.at-s.com/news/article/topics/shizuoka/766582.html

とは言え山は逃げないので気長に待ちましょう。８年前に初めて富士山へ行ったときのことを以下に転載します。以前紹介したとおりこの年は早春に家族で丹沢に行ったり、その後は北八ヶ岳ロープウェイ経由で北横岳へ行ったりしていたので富士山にも家族で挑戦しましたが結果はいかに！？

保育園のクラス会か何かの集まりでミーちゃんパパが「生きてるうちに一回でいいから富士山登りたい」と珍しく断定的な発言をしたのが始まりでした。それを受けて何度か登ったことがあるらしいカナちゃんパパが「そんなん簡単だよ」と言ったので、みんな興味を持ち始め「じゃあ行きましょう！」ということになった。私も富士山に行く機会はそうそうないので家族で行けるところまで参加してみようということになりました。朝３時半に地元のコンビニに集合して車２台で河口湖ICへ。マイカー規制があるため北麓駐車場に停めシャトルバスで富士スバルライン５合目まで。

天気もよく登山日和です。

新型ウイルス COVID-19 の最新研究成果は Kaggle から

６年前に一度だけ機械学習のコンペに参加したことがあります。 

https://yasuabe-ja.blogspot.com/2014/09/higgs-challenge.html 

CERNのATLASチームが取得した衝突データからヒッグス粒子の $H \rightarrow \tau \bar{\tau}$ 崩壊過程の信号を予測しようという興味深いものでした。当時はまだ機械学習があまり話題になっておらずコンペを主催する Kaggle での情報をもとに試行錯誤で解析を行いました。2014年の夏のことですが、あの時はこのコンペのことばかり気になり研究が全くできなくなったので、あれ以来機械学習には深入りしないようにしています。

それでも Kaggle からのメールは時折チェックしていて、最近は新型ウイルス関連のプロジェクトが立ち上がっています。

https://www.kaggle.com/covid19 
https://www.kaggle.com/covid-19-contributions

アカウントを持っているだけで最新の研究成果やデータに直接アクセスできるのでとてもありがたいです。機械学習に興味なくてもとても有益な情報だと思います。

最近は仕事でも機械学習の解析をフォローする必要があり、調べてみると Kaggle について日本語の解説書が出ていたので購入しました。

６年前に知りたかった xgboost のチューニング方法が詳しく紹介されていて、いろいろ思い出しました。実用的でとてもいい入門・解説書だと思います。当時はデータを自前のサーバに落として python を走らせて解析していましたが、今では解析環境を Kaggle が用意してくれているようです。また、GCP(Google Cloud Platform) や AWS(Amazon Web Service) などのクラウドコンピューティングサービスも充実しているので環境条件はとても良くなっています。ネットでも解説記事があるようなので若く時間のある方は是非参加してみてください。 評価指標という明確なルールのもとで最適解を求める能力を競うコンテストなので、多くの理数系の人がおそらく学生の時に参加した「大学への数学」や「高校への数学」の「学コン」みたいなノリで気軽に参加されるといいと思います。成績がいいと国内外の就職にも有利のようですし。

庭木の剪定：ヒイラギモクセイ３

玄関前のヒイラギモクセイを透かし剪定しました。3月に切った時の様子は以下の通り。

写真では分かりづらいですが足元からシマトネリコの枝が生えてきているのでこれからはそれを活かそうと考えました。また高さも思い切って調整して壁側の太い幹を切り落としました。剪定後の様子は以下の通り。

かなりサッパリしました。以前は目隠しの効果を考慮していましたが、足元もスッキリさせました。シマトネリコがだいぶ伸びてきているので見た目も明るく爽やかになった印象です。

庭木の剪定：ハナミズキ２

2年前の秋に剪定して以来です。だいぶ伸びて来てモッサリしてきたので切ることにしました。

剪定前の様子

高さを抑えるために上の枝をバッサリ切り、内側の小枝も処理して、透かし剪定を行いました。途中経過は以下の通り。

2017年夏の至仏山 日帰り：天国のような景色

前回のエントリーで祖母の話が出たので、関連して３年前に行った至仏山日帰り登山の話を以下に転載します。

都内から日帰りで行ける百名山としてあとは蓼科山と上州武尊山かなぁなんて考えながら何度かルートを確認して機会を伺ってましたが、週末はテニスでつぶれることが多くなりなかなか登山に行けてませんでした。そんな頃、テニス仲間の一人が山にも行くそうで、至仏山が良かったというので、計画変更して早速行ってみました。いつものように夜明け前までに登山口に着けるよう2時過ぎに出発しました。沼田ICからさらに長い道のりでやっぱり武尊のほうが近かったかなあなんて思いながらもひたすら尾瀬を目指しました。戸倉駐車場到着前に片側のヘッドライトしかついていない後続車にしばらく付いてこられたのが気になりました。山登る人はそんな車に乗らないだろうし地元の人だとしても朝４時に運転するってどこかで飲んできたのかなあなんてヘンな想像していましたが途中でいなくなったのでたぶん（運転の様子から）地元の若者でしょう。ともかく何とか鳩待峠までの始発バスに間に合いました。

山ノ鼻から山頂へむかう道は登りだけの一方通行なので自然と周回ルートが決まり、まず木道に沿って山ノ鼻へ。東電が作った木道のようです。尾瀬は素晴らしいと聞いていましたが、木道を進みながらだんだんとイメージが現実化してきてワクワクしました。山ノ鼻を曲がったところで山荘の管理人のような方に出会い、「昨日まで雨だったのですが今日は素晴らしいですね。最高です。」と声をかけてもらいました。

確かに夢のような景色でこれが尾瀬か～、遥かな尾瀬～かと感嘆しました。山道に入る前に湿地を少し回り、誰も来ないうちに登り始めました。昨日の雨で川というか滝のようになっている部分もあり、これは一方通行でないとダメだなと理解しました。急坂を何度か登り終え、振り返ると絶景。ここは天国かと思わんばかりでした。

向かい側の燧ケ岳、その手前の尾瀬ヶ原さらには周りを囲む山々、会津駒ヶ岳もハッキリ見え、まさに理想郷でした。何度も振り返り写真を撮りながら登頂。この時のことがとても印象深かったためこのブログのヘッダー（PC版）にはこの時撮った写真を利用しています。

山頂では大学生3人組に写真を撮ってもらいました。

ファーブルの伝記と祖母のこと

今週から下の子がようやく入学式以来、小学校へ登校しました。30人クラスのうち10人だけが順番に登校するという分散登校でした。2時間あまりで下校しましたが、やっとランドセルを使えて嬉しそうでした。やっぱり子供には学校に行ってもらわないと困りますね。この状況、いつまで続くのでしょうか。私が小学校に入ったころは外遊びばかりでしたが、部屋で一人でいるときは図鑑や辞書を眺めることが多かったです。あとポプラ社の伝記だけは買ってもらえたので色々読みました。その中でも心に残っているのがシュバイツァー、ファーブル、ニュートンの伝記です。中学になって引っ越す際に子供用の本は処分することになりましたが、この３つだけは名残惜しくて手元に置くことにしました。

シュバイツァーは時折読み返しました。いつかランバレネに行きたいと思っていましたがいまだに実現できていません。ニュートンについては子供ながらに共感するところがあったのでしょうか、あの時まさか将来物理の研究をするとは思いもよりませんでした。

ファーブルの伝記には特別な思いがあります。私が小学校４，５年生だったでしょうか。母方の祖母が遥々三重県の楠から神戸まで来てくれて何日間か泊まっていきました。その時、祖母が私が学校に行っている間に子供部屋にあった伝記をいくつか読んだそうで、その中でファーブルが一番よかったとこっそり教えてくれたことがありました。楠ではいつもタバコを吸いながらプロレス中継ばかり観ている印象のある祖母がまさか児童書なんか読まないだろうと思っていたので驚いたと同時に私もファーブルの話が大好きだったので嬉しく思いました。祖母は島根県大田市の出身で祖父の仕事の関係か何かで島根で出会って、戦前に三重県までお嫁に来たそうです。母が8歳の時（1958年ごろ）に祖父が亡くなったため、祖母はとても苦労したと聞いています。ファーブルの自伝にも子供のころの信じられない苦労話（10代で一家離散して鉄道建設の肉体労働をしながらも詩心を忘れず苦学して数学・理科の先生になったなど）が出てくるので共感するところが多かったのかもしれません。祖母が亡くなってもう20年近くになりますがあの時神戸に来てくれた祖母のことを今でもたまに思い出します。

Legendre symbols $\lambda_{p} (n )$ for prime $p$ up to 100

前回との関連でCoCalcの計算結果を記録しておきます。$p$ を100までの素数としてルジャンドル記号 $\lambda_{p} (n )$（平方剰余記号とも呼ばれる）が１になるときの $n \in \F_{p}^{\times}$ $(n = 1,2, \cdots, p-1)$ の値を列挙します。ルジャンドル記号の計算コマンドはこちらを参考にしました。

$p$	$n$ for $\lambda_{p} (n) = 1$
2	1
3	1
5	1, 4
7	1, 2, 4
11	1, 3, 4, 5, 9
13	1, 3, 4, 9, 10, 12
17	1, 2, 4, 8, 9, 13, 15, 16
19	1, 4, 5, 6, 7, 9, 11, 16, 17
23	1, 2, 3, 4, 6, 8, 9, 12, 13, 16, 18
29	1, 4, 5, 6, 7, 9, 13, 16, 20, 22, 23, 24, 25, 28
31	1, 2, 4, 5, 7, 8, 9, 10, 14, 16, 18, 19, 20, 25, 28
37	1, 3, 4, 7, 9, 10, 11, 12, 16, 21, 25, 26, 27, 28, 30, 33, 34, 36
41	1, 2, 4, 5, 8, 9, 10, 16, 18, 20, 21, 23, 25, 31, 32, 33, 36, 37, 39, 40
43	1, 4, 6, 9, 10, 11, 13, 14, 15, 16, 17, 21, 23, 24, 25, 31, 35, 36, 38, 40, 41
47	1, 2, 3, 4, 6, 7, 8, 9, 12, 14, 16, 17, 18, 21, 24, 25, 27, 28, 32, 34, 36, 37, 42
53	1, 4, 6, 7, 9, 10, 11, 13, 15, 16, 17, 24, 25, 28, 29, 36, 37, 38, 40, 42, 43, 44, 46, 47, 49, 52
59	1, 3, 4, 5, 7, 9, 12, 15, 16, 17, 19, 20, 21, 22, 25, 26, 27, 28, 29, 35, 36, 41, 45, 46, 48, 49, 51, 53, 57
61	1, 3, 4, 5, 9, 12, 13, 14, 15, 16, 19, 20, 22, 25, 27, 34, 36, 39, 41, 42, 45, 46, 47, 48, 49, 52, 56, 57, 58, 60
67	1, 4, 6, 9, 10, 14, 15, 16, 17, 19, 21, 22, 23, 24, 25, 26, 29, 33, 35, 36, 37, 39, 40, 47, 49, 54, 55, 56, 59, 60, 62, 64, 65
71	1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 19, 20, 24, 25, 27, 29, 30, 32, 36, 37, 38, 40, 43, 45, 48, 49, 50, 54, 57, 58, 60, 64
73	1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 19, 23, 24, 25, 27, 32, 35, 36, 37, 38, 41, 46, 48, 49, 50, 54, 55, 57, 61, 64, 65, 67, 69, 70, 71, 72
79	1, 2, 4, 5, 8, 9, 10, 11, 13, 16, 18, 19, 20, 21, 22, 23, 25, 26, 31, 32, 36, 38, 40, 42, 44, 45, 46, 49, 50, 51, 52, 55, 62, 64, 65, 67, 72, 73, 76
83	1, 3, 4, 7, 9, 10, 11, 12, 16, 17, 21, 23, 25, 26, 27, 28, 29, 30, 31, 33, 36, 37, 38, 40, 41, 44, 48, 49, 51, 59, 61, 63, 64, 65, 68, 69, 70, 75, 77, 78, 81
89	1, 2, 4, 5, 8, 9, 10, 11, 16, 17, 18, 20, 21, 22, 25, 32, 34, 36, 39, 40, 42, 44, 45, 47, 49, 50, 53, 55, 57, 64, 67, 68, 69, 71, 72, 73, 78, 79, 80, 81, 84, 85, 87, 88
97	1, 2, 3, 4, 6, 8, 9, 11, 12, 16, 18, 22, 24, 25, 27, 31, 32, 33, 35, 36, 43, 44, 47, 48, 49, 50, 53, 54, 61, 62, 64, 65, 66, 70, 72, 73, 75, 79, 81, 85, 86, 88, 89, 91, 93, 94, 95, 96

$\la_p (n) \equiv n^{\frac{p-1}{2}}$ $(mod ~ p)$ より

$$\begin{eqnarray}  \la_p (1) &=& 1 \\  \la_p (-1) & =& (-1)^{\frac{p-1}{2}} ~~~ (p \ne 2) \end{eqnarray}$$
が分かる。また、
$$\la_p (2) = (-1)^{\frac{p^{2} -1}{8}} ~~~ (p \ne 2)$$

が知られている。上記のリストからこれらの関係式を確認することが出来る。

Weight-2 dim-1 modular forms with prime levels up to 100

重さ２、次元１でレベルが100までの素数で与えられる保型（モジュラー）形式を調べました。LMFDBの計算結果をこちらにまとめておきます。保型形式を$q$-展開したときの係数 $a_p$（ヘッケ固有値）のリストです。この係数は素数の係数だけからすべて求まるので $p$ として100までの素数を選んでいます。保型形式のレベル $N$ も100までの素数に限定しています。なので $p \ne N$ のとき $gcd(p, N)=1$ です。重さ２の保型形式の場合、解析的ランク(analytic rank)は０か１で与えられ、０と１の場合それぞれについてリストを作成しました。ただし、ここで解析的ランクとは保型形式の$L$-関数の解析的ランクのことで、詳しくはこちらを参照ください。

List of $q$-expansion coefficients $a_p$ for weight-2 dim-1 modular forms with analytic rank 0

$p$ \ $N$	11	17	19	37	67	73	89
2	-2	-1	0	0	2	1	1
3	-1	0	-2	1	-2	0	2
5	1	-2	3	0	2	2	-2
7	-2	4	-1	-1	-2	0	2
11	1	0	3	3	-4	-2	-4
13	4	-2	-4	-4	2	-6	2
17	-2	1	-3	6	3	2	6
19	0	-4	1	2	7	8	-2
23	-1	4	0	6	9	4	2
29	0	6	6	6	-5	2	-6
31	7	4	-4	-4	-10	-2	6
37	3	-2	2	1	-1	-6	10
41	-8	-6	-6	-9	0	6	-6
43	-6	4	-1	8	-2	-2	2
47	8	0	-3	3	-1	6	12
53	-6	6	12	-3	10	10	-6
59	5	-12	-6	12	9	-6	-10
61	12	-10	-1	8	-2	-14	-6
67	-7	4	-4	-4	1	8	12
71	-3	-4	6	-15	0	0	4
73	4	-6	-7	11	-7	1	10
79	-10	12	8	-10	-8	-4	-12
83	-6	-4	12	9	4	-14	-6
89	15	10	-12	6	7	-6	1
97	-7	2	8	8	0	-10	-18

$gcd(m,n)=1$のとき $a_m a_n = a_{mn}$ なので $a_N = 1$ から一般に $a_n$ には$N$倍についてのスケール不変性があることがわかる。$N=11$の場合は、$a_5 = 1$ でもあるため $mod ~ 5$ の性質もあることがわかる。実際、こちらのサイトによると$N=11$の場合は $a_p \equiv p + 1 ~ (mod ~5)$（ただし、$p \ne 11$）となることが Ramanujan によって証明されているそうです。同様にして、$N=37$の場合は $a_p \equiv p + 1 ~ (mod ~3)$（ただし、$p \ne 37$）、$N=73, 89$の場合は$a_p$ $(p \ne N)$ が偶数となることが分かる。また、$N = 17$の時も $a_2 = -1 \equiv 1 ~ (mod ~2)$ なので $a_p$ $(p \ne 2, 17)$ が偶数となる。

なお、これらの係数は $| a_p | \le 2 \sqrt{p}$ を満たすことが知られているが（一般の重さ $k$ の場合は $| a_p | \le 2 p^{\frac{k-1}{2}}$ ）、上のリストもすべてこの条件を満たしていることがわかる。例えば、$|a_p|$が比較的大きい $N=37 , ~ p=71$ の場合も $|a_{71} | = 15 < 2 \sqrt{71} = 16.85  \cdots$ となっている。

次に analytic rank 1 の場合は以下の通り。

特別定額給付金 オンライン申請あれこれ

新型ウイルス対策として社会活動自粛要請を受け、国民１人当たり10万円が政府から給付されることが決まりました。児童手当の給付と同じように市役所から書面で案内があるだろうからそれで申請すればいいやと思っていましたが、義理の両親がオンライン申請を済ませたそうで、それを聞いた妻から家（うち）もヤレとプレッシャーをかけられました。そんな急がなくてもいいんじゃない、いろいろ面倒くさそうだし、以前から何度も頼んでいるのにマイナンバーカードを作ってくれない人に言われたくないわと思いながらも、どうせ暇なんだからそれぐらいやっての暗黙のプレッシャーで渋々調べてみました。

https://kyufukin.soumu.go.jp/ja-JP/index.html

令和2年4月27日において住民基本台帳に記録されている方に、１人につき10万円が給付されます。世帯主の方が、同一世帯全員分の申請を行うことができます。

とのことです。オンラインでやるには世帯主で唯一マイナンバーカードを持っている私が申請するしかありません。愛用のPC(Win7)で申請することにしました。オンライン申請するにはマイナンバーカードのほかに

マイナポータルAPのインストール
マイナンバーカードに対応したICカードリーダライタ

が無いといけません。前者の方は画面の案内に沿ってすぐにインストールできましたが、後者のICカードリーダライタってなに？ ということで調べたところ例えばこちら

https://my-best.com/7199

でマイナンバーカード対応のICカードリーダが紹介されています。安いのから検索しましたがすでに売り切れていたり高額なもの（5000円以上）のものばかりです。しかもWin7に対応しているものは無いようなのでどの機種を買えばいいのかこちら

https://img.myna.go.jp/pdf/iccardreaderwriter.pdf#page=5

で確認しました。1人10万円もらえるにしても3千円払ってその為だけにICカードリーダを購入するのはバカらしいなと考え一先ず保留にしました。

その後、妻にICカードリーダって結構高いけどご両親は持ってるのと聞いたところ昔からe-Taxで使っていて2000円ぐらいだとのことです。なるほど、将来e-Taxで使うこともあるし2000円ぐらいなら買おうかと思い直して調べたところ amazon, rakuten などのメジャーなネットショップでは既に品切れになっているか5000円以上のものばかりでした。やはり皆さんオンライン申請のために購入しているのかなとすこし焦り始めました。ようやくヨドバシのサイトで NTTコミュニケーションズ NTTCommunications ACR39-NTTCom [接触型ICカードリーダライタ]

を見つけて購入しました。

https://www.yodobashi.com/product/100000001002951301/

2,320円（232ポイント付与）でした。5/10時点では「予定数の販売を終了しました」となっています。私は5/9に購入しましたが出荷日時はまだ未定です。とりあえず気長に待つことにしました。（追記：5/12に無事到着しました。）

無線LANルーター買い替え：BUFFALO WZR-450HP から WSR-A2533DHP2

最近、Wi-Fi（無線LANルーター）の調子が悪いので買い替えることにしました。今の家に引っ越す前から使っているのは BUFFALO WZR-450HP

でもう９年目なのでさすがに寿命です。子供のオンライン授業中に接続が切れたりして不便極まりなかったので替えることにしました。アマゾンでお薦めのものにしました。BUFFALO WiFi 無線LAN ルーター WSR-A2533DHP2-CB 11ac ac2600 1733+800Mbps デュアルバンド IPv6対応 日本メーカー 4LDK 3階建向け：

7,630円（タイムセール）でした。昨日の夜、届いたのですがなんだか手間取りそうなので今朝取り替え作業を行いました。久しぶりのことなので付属のセットアップガイドをしっかり読んでから始めました。プロバイダの接続情報も必要になるかもというので一応So-net接続用のID/PWを控えておきました。

2017年夏の男体山 前泊登山

外出自粛中に入山禁止の男体山で遭難・救助されたというニュースを知り、あそこはまだ雪だよなぁなどと思いをはせてしまいました。男体山は二荒山神社（ふたらさんじんじゃ）の御神体なので勝手に登るのは止めましょう。登山口が開いているときは６時開門なので、百名山ハンターの方は急ぎたいかもしれませんが、二荒山神社では駐車場無料、入山料500円で貴重なお守りも貰えるので是非６時まで待ってください。後ろめたい気持ちで登り始めても良いことないって！

さて、３年前の登山の報告は以下の通り。

今回は日光ということで、いろは坂で消耗しそうだし道中も長いので22時過ぎに出発、中禅寺湖畔の歌ヶ浜駐車場で車中泊することにしました。六甲山縦走の時、須磨浦公園駐車場で寝ているので寝られないということはありませんでしたが、今度は周りに車中泊する人たちがおり、その会話が気になりなかなか寝付けませんでした。人気駐車場で泊まる際は駐車位置にも注意が必要です。５時には起床、早めに登山口の二荒山神社へ。

登山口の開門は６時なのでそれまで待ちぼうけでした。当初の計画ではいつものように夜明けとともに登山開始しようと思っていましたが、男体山は二荒山神社のご神体なので失礼のないように６時まで待つことに決めてきました。駐車場で慣れているハイカーから、まあ裏からでも登れるけどねとアドバイスもらい、一瞬ぐらっと来ましたがやめておきました。６時になり記帳、入山料500円を払ってお守りを頂きました。やっぱり６時まで待ってよかったです。普通、お守りだけで500円はするのに登山口直下の駐車場が無料なのだからだいぶ親切です。心置きなく登山開始、これが一番大事！

登山前に宮司さんから説明を受けていたのでルートに迷うことはありませんでした。登り一辺倒で特に後半はあまりなだらかな所はありませんでした。途中、黒や緑の土嚢が破けて山肌が荒れている箇所あり。これだけの山たど神社だけで登山道を管理するのは大変でしょう。（国や県からの補助はあるのでしょうか？）振り返ると雲間から中禅寺湖が眼下に広がっていました。時折湖を見下ろしながら山頂までひたすら登るイメージです。慣れてない方にはきついのではないでしょうか。

山頂には大きな剣が刺さっており、迫力があります。

AviUtlで動画編集あれこれ

前回のエントリーで紹介したようにシジュウカラの巣立ちを動画で撮ったのですが、とてもそのままアップロードできるような内容でなかったので重い腰を上げて動画編集することにしました。調べたところWindowsで無料で動画編集できるAviUtl

http://spring-fragrance.mints.ne.jp/aviutl/

というフリーソフトが解説などもとても充実していて分かり易かったです。

https://sosakubiyori.com/aviutl-introduction/
https://sosakubiyori.com/aviutl-setting/
https://aviutl.info/

いまやYouTuberの時代なのでいまさら動画編集と思われるかもしれませんが、今やらないとこのまま時代に取り残されそうです。デジカメで撮ったmovファイルを編集するには L-SMASH Works File Reader という入力プラグインを入れないといけないのですが、圧縮ファイルの解凍が上手くいきませんでした。そこで、

https://pop.4-bit.jp/?page_id=7929

の下の方にある「通りすがり」さんのコメント(2020-02-01 22:37)を頼りに、Archive Extractorというサイトを使うと解決できました。また、x264guiEx 2.xx のインストールはWindows7では簡易インストーラーが対応していないためこちらで紹介されていたファイルをダウンロードして何とか設定することが出来ました。このファイルは2020/05/19までしかアクセスできないようなので、もしものために一応こちらに保存しました。ちなみに、最新版のAviUtlは対応OSがWin10となっていますがWin7でも動きました。

シジュウカラがやって来た2020：巣立ち、南の空へさようなら！

だんだんとヒナの声が大きくなり巣箱の中でガサゴソと音がするようになりました。5/4のお昼には親鳥がヒナたちに外に出るよう促す声がしきりに聞こえます。いつもはすぐに餌を運んでいたのですが、餌をくわえたままなかなか巣箱に入ろうとしません。巣箱の中も騒々しいです。

そろそろ巣立ちでしょうか。デジカメのバッテリーが切れそうだったので充電して翌日（今日5/5）に備えました。

2年前は午前9時ごろに巣立ったので今度もそれぐらいから待ち構えていました。するとやはり今日が巣立ちの日でした！デジカメのノイズが入ってしまい聞き苦しいですが、動画の編集を初めてやってみました。

ヒナがそこここで鳴いていたので気になって一部動画が揺れてしまいました。今回は時間に追われることがなかったので最後まで見届けることができ感無量です。おっかなびっくりですが、すぐに飛んで行けるのですね。親鳥に見守られながら5，6羽連れ立って南の方へ消えていきました。さようなら！ちょっと寂しくなるね。念のため最後に巣箱を確認しました。

ThunderbirdでGmailを送受信できないときは認証方式をOAuth2に設定してみよう

メーラーとして長年Thunderbirdを利用して Gmail と G Suite (Google Workspace) アカウントを同期させています。

先ほど、メーラーを立ち上げると

メールサーバー pop.gmail.com からの応答: Username and password not accepted.

というエラーが出たので、以前にもあったなあと思いながら検索してみると

https://p2pzen.com/windows/thunderbird-gmail-pop-gmail-com-password/
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q12185874872

というサイトが見つかりました。そうそう、確かグーグルアカウントのセキュリティ設定で

「安全性の低いアプリからのアクセス」を有効

にすれば良かったのだっけということで、有効にしようと思ったのですが設定画面がどうしても開けません。グーグルアカウント設定で本人確認のための電話番語を登録していなかったのでそれが原因かと思いましたが関係ありませんでした。どうやら「安全性の低いアプリからのアクセス」を有効にすること自体が出来なくなったようです。

よく考えるとThunderbirdの送受信の認証方式が「通常のパスワード認証」になっていたことが原因でした。そこで、送信(SMTP)サーバーとサーバ設定のセキュリティ設定を「OAuth2」にすると無事メールの送受信ができるようになりました。Gmailの設定で「メール転送と POP/IMAP」のページから

・すべてのメールで POP を有効にする (ダウンロード済みのメールを含む)
・今後受信するメールで POP を有効にする

のどちらかを選ぶ必要がありますが、上の方を選ぶと古いメッセージを重複して受信してしまうことになるため既存メーラーの設定変更の場合は下の方を選ばないとどえらいことになってしましまうので注意してください。最後にThunderbirdとGmailの同期については例えばこちらのURL

https://www.appsupport.jp/gmail/sync-thunderbird/
https://aprico-media.com/posts/4442

がとても参考になりました。

カローラフィールダーのバッテリー＆タイヤ交換

今朝近所のGSから無料点検案内のハガキが届いたので早速行ってきました。先日、久しぶりに運転したら外付けのカーナビが立ち上がりませんでした。外出自粛で一週間ほど乗っていなかったのでバッテリーの起動がいつもと違い、過電流でも起きたのでしょうか。カーナビ YUPITERU drive navi YPL514SI の電源をいくら押しても何も起こりません。結局、外出中はどうにもならなかったので帰宅後、説明書を読んでカーナビ本体裏側のリセットボタンを（爪楊枝で）押すと無事起動して、ありがたいことに履歴などの設定も保存されていました。このナビは2013年12月に購入したものです。さすがに古いので寿命かなと半ば諦めていましたが無事復活してくれたのでまだまだ利用させてもらいます。新しい道路ができて特に長距離移動ではナビが使えないこともありますが無いよりは断然便利です。地図データを更新できればいいのですがさすがに古い型なので対応していませんでした。買い換えるなら５インチサイズでシンプルなものということで、ユピテル WNL55ML がいいかなと思いますが、まだ新しく道路が出来そうだし妻が新車買いたいとか言っているので、今のが壊れるまで使い倒そうと思います。

My first trip to China in 1996

Camilo José Cela, a Spanish novelist, once wrote in his monumental work "Mazurca para dos muertos" that people all over the world would eventually be eaten by the Chinese. When I read the novel (translated in Japanese) first time more than two decades ago I found the expression funny, ironic and even poetic, yet perceiving some reality of the Chinese culture.

In September 1996 I traveled southern part of China, entering from Hong Kong(香港) and visiting Guangzhou(広州), Guilin(桂林), Yangshuo(陽朔), Hangzhou(杭州), Suzhou(蘇州), Shanghai(上海). This was my first trip to mainland China; HK was not yet China. I stayed a few days in HK to apply for a visa to mainland China. Then I took a train to Guangzhou via Shenzhen(深圳). I went around the busy city of Guangzhou for two days and enjoyed Cantonese cuisine. I then took a long-distance overnight bus to Guilin. A guy next to my sleeping sheet was in a military uniform and probably was in his early 20's.

 near Guilin in 1996

I stayed in the city of Guilin for a day and joined in an excursion trip to a suburban scenic spot together with local families. Although I learned Chinese for one semester apparently I could not make my Chinese (Mandarin) understood at all. So I had to communicate by writing Chinese characters (Kanji) in many occasions. If I remember correctly, I guess, I managed to book a train ticket from Guilin to Hangzhou which departed several days later. I then moved to Yangshuo where a lot of backpackers gathered at that time.

near Yangshuo in 1996

The stay at Yangshuo was fantastic. The rural town was astonishingly westernized; there were bars, movie theaters and cafes that you would never expect to have in other cities in China at that time. I enjoyed river rafting on a swim tube/donut with other backpackers and a local young lady, a university student from Nanning(南寧) who worked part-time there to learn English. After the river rafting I rushed to go back to Guilin so as to take a train which departed that night. Somehow I managed to catch the train where I met a young American traveler who was pursuing PhD in Chinese politics and was surprisingly fluent in Chinese. I waked up early next morning. Landscapes from the train was amazing. Full of rice fields everywhere. I felt I time-tripped to ancient China or Japan. The train arrived in Hangzhou around noon. There I happened to meet a Japanese backpacker and went around the town together. He was also a university student from Nagoya and used to play baseball, so did I. We got along well. He told me about his trip to Urumqi(烏魯木齊) and other places.