前回のエントリーでKメソン(中間子)の話が出てきたので昔のノートを取り出して $K^0 \bar{K^0}$ 系を復習することにしました。孔子の言う「学而時習之」の境地です。中性Kメソンのクォーク構成は $d \bar{s}$ であり、こちらのリストにもあるように$K^0$は擬スカラー中間子なので
\[
K^0 \sim \bar{s} \ga_5 d \, , ~~~~ \bar{K^0} \sim \bar{d} \ga_5 s
\tag{1}
\]
と置ける。ただし、$\ga_5$ は4次元時空でのガンマ行列を用いて $\ga_5 \sim \ga_0 \ga_1 \ga_2 \ga_3$ で与えられる。$K^0 \bar{K^0}$ 系は自然現象の $CP$ 対称性が保存されていないことが初めて実験により確認されたという点でとても重要です。この発見自体は1964年ですが、1980年にこの成果によりCroninとFitchが1980年にノーベル賞受賞しました。2000年代にはBファクトリーと呼ばれる実験施設(SLACおよびKEK)で大量の中性 $B$ メソン $( B^0 \sim \bar{b} \ga_5 d$, $B_s^0 \sim \bar{b} \ga_5 s )$ が生成され、$B^0 \bar{B^0}$ 系での $CP$ 対称性の破れが確認されました。この $CP$ 対称性の破れを標準模型の枠組みで説明したのが我々日本人にはなじみ深い小林・益川モデルです。(2008年ノーベル賞受賞。このときKEKでのBelle実験の成果が受賞のはずみになった旨が報道されていました。益川先生ノーベル賞記念講演の日本語原稿はこちらです。)$CP$ 対称性の破れは理論上は存在してもおかしくない反物質がなぜ我々の世界には見られないのかを説明する有力な手掛かりとなっているためその現象の実験的・理論的な解明は今もなお素粒子理論研究の重要な分野の1つです。実際、ごく最近にも中性Dメソン $( D^0 \sim \bar{u} \ga_5 c )$ の崩壊過程の観測からcharmクォークが関与するハドロンの崩壊過程における$CP$対称性の破れが初めて確認されました。(論文はこちら、その意義についての相原博昭先生による解説はこちらから。)
\[
K^0 \sim \bar{s} \ga_5 d \, , ~~~~ \bar{K^0} \sim \bar{d} \ga_5 s
\tag{1}
\]
と置ける。ただし、$\ga_5$ は4次元時空でのガンマ行列を用いて $\ga_5 \sim \ga_0 \ga_1 \ga_2 \ga_3$ で与えられる。$K^0 \bar{K^0}$ 系は自然現象の $CP$ 対称性が保存されていないことが初めて実験により確認されたという点でとても重要です。この発見自体は1964年ですが、1980年にこの成果によりCroninとFitchが1980年にノーベル賞受賞しました。2000年代にはBファクトリーと呼ばれる実験施設(SLACおよびKEK)で大量の中性 $B$ メソン $( B^0 \sim \bar{b} \ga_5 d$, $B_s^0 \sim \bar{b} \ga_5 s )$ が生成され、$B^0 \bar{B^0}$ 系での $CP$ 対称性の破れが確認されました。この $CP$ 対称性の破れを標準模型の枠組みで説明したのが我々日本人にはなじみ深い小林・益川モデルです。(2008年ノーベル賞受賞。このときKEKでのBelle実験の成果が受賞のはずみになった旨が報道されていました。益川先生ノーベル賞記念講演の日本語原稿はこちらです。)$CP$ 対称性の破れは理論上は存在してもおかしくない反物質がなぜ我々の世界には見られないのかを説明する有力な手掛かりとなっているためその現象の実験的・理論的な解明は今もなお素粒子理論研究の重要な分野の1つです。実際、ごく最近にも中性Dメソン $( D^0 \sim \bar{u} \ga_5 c )$ の崩壊過程の観測からcharmクォークが関与するハドロンの崩壊過程における$CP$対称性の破れが初めて確認されました。(論文はこちら、その意義についての相原博昭先生による解説はこちらから。)
$CP$ 対称性の破れという言葉は何度も聞いたことがあっても専門家でない限りなかなかその真髄は分かりません。私も学部生の時に前述の相原先生の素粒子物理概論という講義で初めて $CP$ 対称性の破れについて聴いたときは、その意味がさっぱり分からず理解不能でした。物理なのだから第一原理(ラグランジアン)から考えれば分かるはずなのですが、そのラグランジアンが書き下されていないので困りました。そこで、当時書店にあった坂井典佑先生の『素粒子物理学 (物理学基礎シリーズ)』を購読してみると、そのようなラグランジアンは素粒子物理学の標準模型で与えられ、それを理解するには場の量子論でゲージ理論をマスターする必要があることを知りました。結局、大学院で場の理論を勉強してようやく $CP$ 対称性の破れについて理解できたような気がします。
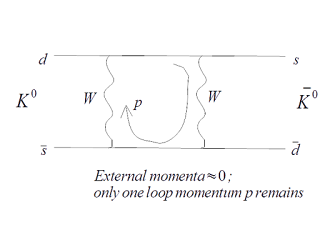
$K^0 \bar{K^0}$ の混合は$s$クォークが $| \Del s | =2$ だけ変化する以下のファインマン図で表される散乱過程を評価することで解析できる。
$K^0$ の崩壊に関与する相互作用は標準模型から
\[
{\cal L}_{int} = - \frac{g}{\sqrt{2}}
\left( W^{+}_{\mu} \bar{U}^{i} \ga_\mu \frac{1 - \ga_5}{2} D^{j} V_{ij} +
W^{-}_{\mu} \bar{D}^{j} \ga_\mu \frac{1 - \ga_5}{2} U^{i} V_{ij}^{*} \right)
\tag{2}
\]
で与えられる。ここで、$U^i = (u, c, t)$, $D^i = (d, s, b)$ はそれぞれ3世代クォークのペアを表し、$V_{ij}$ はCKM(Cabibbo-Kobayashi-Maskawa)行列の行列要素、$g$ は弱い相互作用の結合係数、$W^{\pm}$ はWボソンを表す。上図の1ループ・ファインマン図で外線 ($d, s$とその反粒子) の運動量はWボソンの質量 $M_W$ や重いクォークの質量に比べて無視できるので、$| \Del s | =2$ となる $K^0 \bar{K^0}$ 混合を記述する有効ラグランジアンは
\[
{\cal L}_{eff}^{| \Del s | =2} = - C \, \bar{s} \ga_\mu (1 - \ga_5 ) d \, \bar{s} \ga_\mu (1 - \ga_5 ) d + h.c.
\tag{3}
\]
となることが導出できる。その詳細については専門家による解説
を参照されたい。特にサイエンス社の教科書はこの計算の第一人者(の1人)である林(Lim)先生によるもので歴史的な経緯に沿ってとても詳しい解説がなされているので興味ある方は是非手に取ってもらいたい。上式(3)の係数 $C$ はループ運動量の積分から求められ、
\begin{eqnarray}
C &=& {G_F}^2 \sum_{i,j} \la_i \la_j \int \frac{d^4 p}{(2 \pi)^4}
\frac{p^2 M_W^4}{(p^2 + {M_W}^2 )^2 (p^2 + {m_i}^2 )^2 (p^2 + {m_j}^2 )^2 }
\nonumber \\
&=& \frac{{G_F}^2 M_W^2 }{16 \pi^2} \sum_{i,j} \la_i \la_j \, A_{ij}
\tag{4} \\
A_{ij} &=& \left[
\frac{1}{ 1 - x_i } + \frac{ {x_i}^2 \log x_i }{ (1 - x_i )^2 }
\right] -
\left[
\frac{1}{ 1 - x_j } + \frac{ {x_j}^2 \log x_j }{ (1 - x_j )^2 }
\right]
\tag{5}
\end{eqnarray}
と表せる。ただし、$\la_i = V_{i 1} V_{i 2}^{*}$, $x_i = \frac{m_i^2}{M_W^2}$ である。$G_F$ はフェルミ結合定数 $G_F = \frac{\sqrt{2}}{8}\frac{g^2}{M_W^2}$ である。こちらを参照するとクォークの質量($MeV$単位)は $m_u \approx 2.4$, $m_d \approx 4.8$, $m_s \approx 104$, $m_c \approx 1270$, $m_b = 4680$, $m_t \approx 171200$ で与えられ、Wボソンの質量は $M_W \approx 80400 [MeV]$ なので $\frac{m_u}{M_W} \approx 0$, $\frac{m_c}{m_t} \ll 1$ と近似すると
\[
C \approx \frac{{G_F}^2}{16 \pi^2} \left[
\la_2^2 m_c^2 + \la_3^2 m_t^2 + \frac{2 \la_2 \la_3 }{1 - \left( \frac{m_c}{m_t} \right)^2 } m_c^2 \log \left( \frac{m_c}{m_t} \right)^2
\right]
\tag{6}
\]
が得られる。ただし、上で定義したように $\la_2$, $\la_3$ はCKM行列要素で与えられる。
\begin{eqnarray}
\la_2 &=& V_{21} V_{22}^{*} = s_1 c_2 (c_1 c_2 c_3 - s_2 s_3 e^{-i \del})
\nonumber \\
\la_3 &=& V_{31} V_{32}^{*} = s_1 s_2 (c_1 s_2 c_3 + c_2 s_3 e^{-i \del})
\tag{7}
\end{eqnarray}
従って、位相 $\del$ がゼロでなければ $C$ は複素数となり、このことから $K^0 {\bar K}^0$ 混合で $CP$ 対称性が破れていることが議論されるのが一般的である。
ここでは議論を簡単にするため $K^0$ メソン系の低エネルギー有効作用を使ってラグランジアンが$CP$対称性を破ることを直接見てみよう。$\pi^0 , K^0$ など擬スカラーメソンの有効作用は標準模型のQCDラグランジアンに現れるカイラル対称性の自発的な破れ
\[
G= U(3)_L \times U(3)_R \longrightarrow H = U(3)_{L+R}
\tag{8}
\]
にゴールドストン定理を適用することで得られる。元となるカイラル対称性は $m_u$, $m_d$, $m_s$ が同じ質量をもつことを仮定しているので実際には完全な対称性ではない。そのため、生成される南部-ゴールドストンボソンは質量を持つがそのエネルギースケール ($m_{\pi} \approx 140 MeV$) は強い相互作用によってカイラル対称性が破れるエネルギースケール $1 GeV$ に比べると1オーダー小さい。これらは擬南部-ゴールドストン粒子と呼ばれ9つのメソン $\left( \pi^{\pm}, \pi^0 , K^{\pm}, K^0 , {\bar K}^0 , \eta , \eta^\prime \right)$ に対応する。ゴールドストンの定理より南部-ゴールドストン粒子 $\varphi$ の低エネルギー有効ラグランジアンは
\[
{\cal L}_{GB} = \frac{f^2}{2} \d_\mu \varphi \d^\mu \varphi + {\cal O}(\varphi^3 )
\tag{9}
\]
($f$ は定数)で与えられる。(これは標的空間が $G/H$ の非線形シグマ模型とみなせる。)また、南部-ゴールドストン粒子 $\varphi$ の運動方程式はカレント $J_\mu = f^2 \d_\mu \varphi + {\cal O}(\varphi^2 )$ の保存則 $\d_\mu J^\mu = 0$ で与えられる。$K_0$ メソンの場合、対応するカレントは
\[
J^{K^0}_{\mu} \simeq f_K \d_\mu K^0 + \cdots
\tag{10}
\]
($f_K = 156 [MeV] $ は $K^0$ の崩壊定数)となる。この点について詳細はナイアの教科書
の309ページを参照してください。このカレントは軸性(axial)カレント $J^{(A)K^0}_{\mu} = \bar{s} \ga_\mu \ga_5$ に対応するので $K^0 {\bar K}^0$ 系の低エネルギーでは $\bar{s} \ga_\mu \ga_5 d \longrightarrow f_K \d_\mu K^0$ とおける。よって、(3)式の ${\cal L}_{eff}^{| \Del s | =2} $ はこのエネルギーレベルで
\[
{\cal L}_{eff}^{| \Del s | =2} \longrightarrow
{\cal L}_{eff}^{K^0 {\bar K}^0} \simeq C f_K^2 m_K^2 K^0 K^0
+ C^* f_K^2 m_K^2 {\bar K}^0 {\bar K}^0
\tag{11}
\]
となる。$m_K$ は $K^0$ メソンの質量 $m_K = 497 [MeV]$ である。ここで、擬南部-ゴールドストン粒子である $K^0$ の運動方程式は $K^0$ が質量を持つため(軸性)カレントの保存則では表せないこと
\[
\d_\mu J^{K^0 \mu} \simeq f_K \d^2 K^0 + \cdots \simeq - f_k m_K^2 K^0
\tag{12}
\]
に注意しよう。このようにカレントは保存しないが、$K^0$ の質量による非保存の効果は小さいと期待される。というのも、ゴールドストン定理を$(8)$に適用するにあたり、メソンの質量項は(第一近似では)無視できるとして議論したからである。その意味で関係式(12)は PCAC (Partial Conservation of Axial-vector Current) と呼ばれる。
最後に ${\cal L}_{eff}^{K^0 {\bar K}^0}$ の $CP$ 変換を考える。$K^0$ メソンが擬スカラー粒子(1)であることを用いると、$CP$ 変換された $K^0$ メソンは
\[
K_{CP}^{0} = - {\bar K}^0 \, , ~~~~ {\bar K}^{0}_{CP} = - K^0
\tag{13}
\]
となる。これより $K^0 {\bar K}^0$ 系の有効作用
\[
S_{eff}^{K^0 {\bar K}^0} (K^0, {\bar K}^{0}, f_K, m_K, C)
= \int d^4 x ~ {\cal L}_{eff}^{K^0 {\bar K}^0}
\tag{14}
\]
ここでは議論を簡単にするため $K^0$ メソン系の低エネルギー有効作用を使ってラグランジアンが$CP$対称性を破ることを直接見てみよう。$\pi^0 , K^0$ など擬スカラーメソンの有効作用は標準模型のQCDラグランジアンに現れるカイラル対称性の自発的な破れ
\[
G= U(3)_L \times U(3)_R \longrightarrow H = U(3)_{L+R}
\tag{8}
\]
にゴールドストン定理を適用することで得られる。元となるカイラル対称性は $m_u$, $m_d$, $m_s$ が同じ質量をもつことを仮定しているので実際には完全な対称性ではない。そのため、生成される南部-ゴールドストンボソンは質量を持つがそのエネルギースケール ($m_{\pi} \approx 140 MeV$) は強い相互作用によってカイラル対称性が破れるエネルギースケール $1 GeV$ に比べると1オーダー小さい。これらは擬南部-ゴールドストン粒子と呼ばれ9つのメソン $\left( \pi^{\pm}, \pi^0 , K^{\pm}, K^0 , {\bar K}^0 , \eta , \eta^\prime \right)$ に対応する。ゴールドストンの定理より南部-ゴールドストン粒子 $\varphi$ の低エネルギー有効ラグランジアンは
\[
{\cal L}_{GB} = \frac{f^2}{2} \d_\mu \varphi \d^\mu \varphi + {\cal O}(\varphi^3 )
\tag{9}
\]
($f$ は定数)で与えられる。(これは標的空間が $G/H$ の非線形シグマ模型とみなせる。)また、南部-ゴールドストン粒子 $\varphi$ の運動方程式はカレント $J_\mu = f^2 \d_\mu \varphi + {\cal O}(\varphi^2 )$ の保存則 $\d_\mu J^\mu = 0$ で与えられる。$K_0$ メソンの場合、対応するカレントは
\[
J^{K^0}_{\mu} \simeq f_K \d_\mu K^0 + \cdots
\tag{10}
\]
($f_K = 156 [MeV] $ は $K^0$ の崩壊定数)となる。この点について詳細はナイアの教科書
の309ページを参照してください。このカレントは軸性(axial)カレント $J^{(A)K^0}_{\mu} = \bar{s} \ga_\mu \ga_5$ に対応するので $K^0 {\bar K}^0$ 系の低エネルギーでは $\bar{s} \ga_\mu \ga_5 d \longrightarrow f_K \d_\mu K^0$ とおける。よって、(3)式の ${\cal L}_{eff}^{| \Del s | =2} $ はこのエネルギーレベルで
{\cal L}_{eff}^{| \Del s | =2} \longrightarrow
{\cal L}_{eff}^{K^0 {\bar K}^0} \simeq C f_K^2 m_K^2 K^0 K^0
+ C^* f_K^2 m_K^2 {\bar K}^0 {\bar K}^0
\tag{11}
\]
となる。$m_K$ は $K^0$ メソンの質量 $m_K = 497 [MeV]$ である。ここで、擬南部-ゴールドストン粒子である $K^0$ の運動方程式は $K^0$ が質量を持つため(軸性)カレントの保存則では表せないこと
\[
\d_\mu J^{K^0 \mu} \simeq f_K \d^2 K^0 + \cdots \simeq - f_k m_K^2 K^0
\tag{12}
\]
に注意しよう。このようにカレントは保存しないが、$K^0$ の質量による非保存の効果は小さいと期待される。というのも、ゴールドストン定理を$(8)$に適用するにあたり、メソンの質量項は(第一近似では)無視できるとして議論したからである。その意味で関係式(12)は PCAC (Partial Conservation of Axial-vector Current) と呼ばれる。
最後に ${\cal L}_{eff}^{K^0 {\bar K}^0}$ の $CP$ 変換を考える。$K^0$ メソンが擬スカラー粒子(1)であることを用いると、$CP$ 変換された $K^0$ メソンは
\[
K_{CP}^{0} = - {\bar K}^0 \, , ~~~~ {\bar K}^{0}_{CP} = - K^0
\tag{13}
\]
となる。これより $K^0 {\bar K}^0$ 系の有効作用
\[
S_{eff}^{K^0 {\bar K}^0} (K^0, {\bar K}^{0}, f_K, m_K, C)
= \int d^4 x ~ {\cal L}_{eff}^{K^0 {\bar K}^0}
\tag{14}
\]
の $CP$ 変換は $ S_{eff}^{K^{0} {\bar K}^{0} } (K^{0}_{CP} , {\bar K}^{0}_{CP}, f_K, m_K, C^* )$ で与えられる。よって、$C$ が実数なら $K^0 {\bar K}^0$ 系の有効作用の $CP$ 対称性は保存されるが、実際にはCKM行列要素の精密な観測から $C$ は複素数となることが分かっているため、$K^0 {\bar K}^0$ 系有効作用の $CP$ 対称性は破れていることがわかる。この議論はクォークレベルでのラグランジアン(2)でも成り立つことが知られている。次回のエントリーではそのあたりのことをもう少し丁寧に見ていくことにしよう。




0 件のコメント:
コメントを投稿